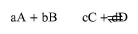
eq. (A.47)
This operation can handle any number of equilibrium reactions and supports a wide variety of reaction equilibrium expressions. It computes the conversion for any number of simultaneous reactions based on the equilibrium constants, the stoichiometric coefficients, and the component concentration exponents that the user specifies.
● Batch Vessel Procedure in a Reactor
● Batch Vessel Procedure in a Seed Reactor
● Batch Vessel Procedure in a Bioreactor
● Batch Vessel Procedure in a Seed Bioreactor
● Batch Vessel Procedure in a Disposable Bioreactor
● Batch Vessel Procedure in a Disposable Seed Bioreactor
● Batch Vessel Procedure in a Fermentor
● Batch Vessel Procedure in a Seed Fermentor
● Batch Vessel Procedure in a Disposable Bioreactor
● Inoculum Preparation Procedure in a Rocking Bioreactor
● Inoculum Preparation Procedure in a Roller Bottle
● Inoculum Preparation Procedure in a T-Flask
● Inoculum Preparation Procedure in a Shake Flask
● Inoculum Preparation Procedure in a Test Tube
● Batch 1x1 Generic Box Procedure
● Batch 3x3 Generic Box Procedure
● Batch 5x5 Generic Box Procedure
● Batch 10x10 Generic Box Procedure
Consider the following equilibrium reaction
|
|
eq. (A.47) |
Define the extent of reaction, ξ, as follows:
|
|
eq. (A.48) |
If νi is the stoichiometric coefficient of component i (negative for reactants, positive for products), the above equation can be rewritten as
|
|
eq. (A.49) |
and for multiple reactions, the above equation becomes:
|
|
eq. (A.50) |
where:
● q is the number of simultaneous reactions,
● ni0 is the mole flowrate of component i in the feed, and
● ni is the mole flowrate of component i in the outlet stream (at equilibrium).
Further, for each reaction j we have the equilibrium relationship which can be written as:
|
|
eq. (A.51) |
If ξ= [ξ1, ξ2, ..., ξq] is used as a vector of independent variables with an initial value of zero, the above equations become equivalent to a system of nonlinear algebraic equations which are solved numerically for ξ. Substitution of the calculated ξ values into the above equations yields the composition of the reaction mixture at equilibrium. For the non-isothermal case, the temperature of the mixture T is another unknown and the energy balance relationship provides the additional equation for solving the system.
To account for emissions, the user can specify the percentage of each component that is emitted. Please note that the specified percentage is based on the composition of the reaction mixture after equilibrium is reached.
The equilibrium reactor can operate isothermally, adiabatically or with a specified heating or cooling duty. For adiabatic operation or for specified heating or cooling duty, the equilibrium temperature is an unknown variable that is calculated by the model. For isothermal operation (specified operating temperature), the energy balance equation is used to calculate the heating or cooling requirement.
The average agitation power is estimated by multiplying the agitation rate (kW/m3 of liquid mixture) by the total liquid volume of the step. It is assumed that all agitation power eventually dissipates into heat that contributes to the heating or cooling requirements of the step.
See Batch Vessel Operations: Equipment Sizing.
See Vacuum Pump Auxiliary Equipment Calculations.
1. Fogler, H. S. 1992. Elements of Chemical Reaction Engineering, 2nd edition, Prentice Hall.
The interface of this operation has the following tabs:
● Oper. Cond’s, see Batch Reaction Operations: Oper. Conds Tab
● Volumes, see Batch Vessel Operations: Volumes Tab
● Reactions, see Equilibrium Reaction Operations: Reactions Tab
● Vent/Emissions, see Reaction Operations: Vent/Emissions Tab
● Labor, etc, see Operations Dialog: Labor etc. Tab
● Description, see Operations Dialog: Description Tab
● Batch Sheet, see Operations Dialog: Batch Sheet Tab
● Scheduling, see Operations Dialog: Scheduling Tab