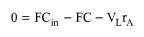
eq. (A.59)
The continuous fermentation model handles any number of reactions and supports a wide variety of fermentation kinetics. The inlet stream(s) is/are assumed to be perfectly (and instantaneously) mixed with the material already in the reactor, so that the outlet stream composition is identical to that of the reactor contents.
● Continuous Kinetic Reaction Procedure in a Fermentor
For a component A that enters a continuous fermentor, the component balance equation is given by the following equation:
|
|
eq. (A.59) |
where F is the volumetric flowrate, Cin is the inlet concentration of component A, C is the outlet concentration of component A, and rA is the combined reaction rate of component A, given by:
|
|
where rAj is the reaction rate of component A due to reaction j and q is the overall number of reactions. If K is the rate reference component of reaction j, then, the reaction rate of component A due to reaction j is given by the following equation:
|
|
where νAj and νkj are the stoichiometric coefficients of components A and K in reaction j and can be specified on mass or molar basis. Negative stoichiometric coefficients are used for reactants and positive for products. The general rate expression (based on the rate reference component) of a reaction j is given by the following equation:
|
|
where a and b are constants and μmax is the maximum specific biomass growth rate. S1, S2 and S3 terms represent the kinetic expressions of three different components (e.g., substrates or reaction products) (S3 term can be used specifically for the inhibitor component). Finally, the B-Term represents the kinetic expression of the biomass component. The kinetic expression options for S1, S2 and S3 terms include Monod, Haldane (with product inhibition), Inhibition first order, and none.
The above equations written for each component entering a continuous fermentor constitute a set of non-linear equations, which is solved numerically to calculate the outlet stream concentration.
To account for emissions, the user can specify the percentage of each component that is emitted. Please note that the specified percentage is based on the composition of the outlet stream.
energy balances are performed that take into account the heat of reaction, the agitation power (it is assumed that all agitation power dissipates into heat), and the sensible heat of input and output streams. The model estimates the required heating or cooling duty under certain operating conditions.
The average agitation power is estimated by multiplying the unit power requirement (kW/m3 of liquid mixture) by the liquid volume.
Equipment purchase cost is based on total vessel volume, agitation power and material of construction. The equipment purchase cost includes the cost of the vessel along with the agitator cost. If the vessel is checked as an ‘ASME Vessel’ (i.e., constructed according to standards published by the American Society of Mechanical Engineers) then it is assumed to withstand pressure to 35 psig and its purchase cost is penalized by 20% over the base vessel cost. If the operating pressure of the vessel is set to a pressure higher than 3 atm, then the vessel’s purchase cost is penalized by an 80% increase over the base cost.
See Vessel Sizing (Continuous Operations).
See Vacuum Pump Auxiliary Equipment Calculations.
1. Fogler, H. S. 1992. Elements of Chemical Reaction Engineering, 2nd edition, Prentice Hall.
The interface of this operation has the following tabs:
● Oper. Cond’s, see Continuous Fermentation Operations: Oper. Conds Tab
● Volumes, see Continuous Vessel Operations (Design Mode): Volumes Tab and Continuous Vessel Operations (Rating Mode): Volumes Tab
● Reactions, see Kinetic Reaction/Fermentation Operation: Reactions Tab
● Split, see Continuous Reaction / Storage Operations: Split Tab
● Vent/Emissions, see Reaction Operations: Vent/Emissions Tab
● Labor, etc, see Operations Dialog: Labor etc. Tab
● Description, see Operations Dialog: Description Tab
● Batch Sheet, see Operations Dialog: Batch Sheet Tab
● Scheduling, see Operations Dialog: Scheduling Tab