Use this operation to concentrate a solution by continuous evaporation of solvent(s) in a multi- effect evaporator. The heat required to raise the temperature of the solution to its boiling point in the evaporator is provided by a heating agent and, optionally, by vapor recompression. In the overwhelming majority of evaporations the solvent is water and the heating agent is steam.
● Multi-Effect Evaporation Procedure
|
Term |
Description |
|
|
|
|
Condensing Temperature of Heating Fluid in First Effect |
Estimate of temperature in heating space of first effect. The evaporator design is based on the heat exchanger design equation (Q=UAΔT). Based on this equation, the heat transfer area (A) of each effect can be calculated based on the heat transfer rate (Q), the overall heat transfer coefficient (U), and the temperature difference (ΔT) between the hot-side stream (heating fluid that flows in the heating space) and the cold-side stream (solution) for that effect. For each effect, the program uses the temperature of the concentrated solution as an estimate of the cold-side stream and the condensing temperature of the heating fluid at the pressure it exhibits in the heating space of that effect as an estimate of the temperature of the hot-side stream. For the first effect, the heating fluid may consist of heating agent and/or recompresesed vapor (if vapor recompression is employed) and/or desuperheating agent (if mechanical vapor recompression and a desuperheating agent are employed). |
|
Effect |
Each evaporator in the sequence of evaporators that comprise a multi-effect evaporator. |
|
Evaporation Capacity |
The total mass evaporation rate of all solvents (i.e., the sum of the mass evaporation rates of all volatile components in all effects.) |
|
Evaporation Economy |
The ratio of evaporation capacity to heating agent consumption rate. |
|
Evaporation Percentage |
The percent ratio of total mass evaporation rate to initial mass flow rate in the feed stream for a particular solvent (i.e., volatile component). |
|
Forward / Backward Feed Flow Arrangement |
The usual method of feeding a multi-effect evaporator is to pump the feed solution into the first effect and send it in turn through the other effects. This is called forward feed. The transfer of the liquid from effect to effect can be done without pumps, since the flow is in the direction of decreasing pressure. Another common method is backward feed, in which dilute liquid is fed to the last effect and then is pumped through the successive effects to the first. This method requires a pump between each pair of effects. |
|
Liquor |
The concentrated solution produced by each evaporator. |
|
Mechanical Vapor Recompression (MVR) |
In mechanical vapor recompression, a fraction of vapor produced in a single evaporator or in the last effect of a multi-effect evaporator is transferred to an implicit compressor, where it is recompressed. The compressed vapor is then used to boil the solution in the first effect together with “make-up” steam (or other heating agent). In addition, a desuperheating agent may be added to the mixture of recompressed vapor and make-up steam before it enters the first effect in order to improve the heat transfer coefficient in the first effect. |
|
Multi-Effect Evaporation (MEE) |
Evaporation performed in a sequence of evaporators connected together in such a way that the concentrated solution in one is fed to another and the vapor produced by one can be used to boil the solution in another. Each evaporator in this sequence is called an effect. The heat required to boil the solution in the first effect is provided by a heating agent. A condenser is implied after the last effect to enable heat transfer in all effects after the first one. |
|
Relative Mass Evaporation Rate |
The ratio of the evaporation percentage of a solvent (i.e., volatile component) to the largest evaporation percentage among all solvents. |
|
Thermal Vapor Recompression (TVR) |
In thermal vapor recompression, a fraction of vapor produced in a single evaporator or in a particular effect of a multi-effect evaporator (usually the first one) is transferred to an implicit steam ejector, where it is recompressed using “motive” steam (or other heating agent). The compressed mixture is then used to boil the solution in the first effect. |
The solution to be concentrated is fed continuously to the hosting equipment through the ‘Feed’ input port. Note that the hosting equipment may be a single-effect evaporator or a multi-effect evaporator (i.e., a sequence of two or more evaporators in series called effects). For simplicity, the hosting equipment is named “Multi-Effect Evaporator”.
During this operation, a fraction of the solvent contained in the feed is evaporated continuously thus producing vapor and concentrated solution (“liquor”) at the outlet. If two or more effects are used, then the vapor produced in one effect can be used to boil the solution in another effect. That is, the vapor produced in one effect is fed to the heating space of another effect and there it becomes condensed. The condensed vapor leaving each effect is transferred out of through the “Condensed Vapor” output port. If vapor recompression is employed, then part (or all) of the vapor produced may be recovered, recompressed and fed to the heating space of the first effect, where it becomes condensed. This is also transferred out through the “condensed vapor” output port.
To summarize, the following streams may be present at the outlet: vapor, concentrated solution and condensed vapor. These are transferred out of the equipment continuously using the following ports:
● The outlet vapor (i.e., the fraction of total vapor produced that is not condensed) is transferred out through the designated output port for vapor named ‘Vapor’ (top).
● The concentrated solution is transferred out through the designated output port for liquor named ‘Liquor’ (bottom).
● The condensed vapor (i.e., the fraction of total vapor that becomes condensed vapor in the heating space of one or more effects) is transferred out through the designated output port for condensed vapor named ‘Condensed Vapor’ (middle).
Any vapor present in the feed stream is ignored in evaporation calculations and it is simply sent to the vapor stream. In other words, all evaporation calculations are based on the liquid/solid portion of the feed stream only. For example, if 20% of water in the feed is already vapor and the evaporation% of water in the evaporator is set to 10%, then a further 10% of the remaining 80% of liquid water (or a further 8% of the total amount of water in the feed) will be vaporized, resulting in a total 28% of water contained in the feed to be in the vapor phase inside the evaporator.
The condensed vapors coming out of each effect are mixed adiabatically and the mixture is sent to the ‘Condensed Vapor’ stream. The pressure of that stream is assumed to be equal to the ambient pressure.
The heat required to raise the temperature of the solution to its boiling point in the first effect is provided by a heating agent and, optionally, by vapor recompression. As with any other heat transfer agent in the program, there are no explicit input/output ports for the supply/return of heating agent to/from the evaporator. The user simply selects a heating agent for this operation through the corresponding data dialog (for an example, see Multi-Effect Evaporation: Heating Tab). Consequently, there will be no heating agent in the condensed vapor stream leaving the first effect through the ‘Condensed Vapor’ port. This stream may only contain the recompressed vapor used in the heating space of the first effect (if any).
The same remarks apply to the desuperheating agent (if available) as well.
In order for evaporation to take place, a temperature difference must exist between heating fluid and solution in each effect. Typically, a condenser is used to condense the outlet vapor and also to achieve the temperature differences required in order for the evaporation to take place in each effect. For simplicity, this step is omitted in the current model. In other words, although the presence of a condenser is implied in such cases (since it is required for evaporation to occur), the contents of the vapor stream are assumed to be those before condensation. However, if you wish to account for the presence of a downstream condenser, you may add a Condensation procedure (see Condensation Procedure) after the Multi-Effect Evaporation procedure, and use it to condense the contents of the vapor stream.
Below, the contents of all output streams in case of a single- or multi-effect evaporator with or without vapor recompression are described in more detail:
In the simplest case where there is a single evaporator, the heat required to boil the solution is provided by a heating agent, which is supplied continuously to the heating space of the evaporator. The entire amount of vapor produced in the evaporator leaves the evaporator through the ‘Vapor’ port. The concentrated liquor leaves the evaporator through the ‘Liquor’ port. Since there is no condensed vapor, there is no need to add a stream to the ‘Condensed Vapor’ port in this case.
To indicate that the equipment contains only one effect, the ‘Evaporation Data (Per Effect)’ table shown in the Effects tab of this operation’s data dialog must contain only one row (see Multi-Effect Evaporation: Effects Tab).
To indicate that no vapor recompression is employed, ‘None’ must be selected in the Vapor Recompression Options that are available in the Oper. Conds Tab of the same dialog (see Multi-Effect Evaporation: Oper. Conds Tab).
if a single-effect evaporator is used, and vapor recompression is employed, a fraction of the vapor phase may be recovered, recompressed and used as heating fluid in the heating space of the evaporator, where it becomes condensed vapor. This amount of vapor which is recompressed and then condensed, leaves the evaporator through the ‘Condensed Vapor’ port. The remaining vapor eaves the evaporator through the ‘Vapor’ port. Finally, the concentrated liquor leaves the evaporator through the ‘Liquor’ port.
In order to model vapor recompression, either ‘Mechanical Vapor Recompression’ or ‘Thermal Vapor Recompression’ must be selected in the Vapor Recompression Options that are available in the Oper. Conds Tab of the operation’s data dialog (see Multi-Effect Evaporation: Oper. Conds Tab).
If mechanical vapor recompression is used, the recompressed vapor may be optionally mixed with desuperheating agent. If the heat supplied by this mixture is less than that required for the evaporation, then a “make-up” heating agent is added to the mixture in order to supply the extra heat.
On the other hand, if thermal vapor recompression is used, the vapor is mixed with “motive” heating agent in a steam ejector and the mixture is used as heating fluid in the heating space of the evaporator. The amount of vapor that is recompressed is such that the total heat supplied by the mixture of heating agent and recompressed vapor in the heating space of the evaporator matches the heating requirement for the evaporation.
If a multi-effect evaporator is used, a heating agent is used in the first effect to supply the heat required to boil the solution in that effect. The effects are connected together in such a way that the concentrated solution coming out of each effect is either fed to the next effect (according to the flow of vapor) if forward feed flow arrangement is used, or to the previous effect if backward feed flow arrangement is used. Also, the vapor produced by each effect is fed to the heating space of the next effect in order to boil the solution in that effect, and therefore, it leaves the heating space of that effect as condensed vapor. The individual condensed vapors from all effects are then mixed together non-adiabatically (by assuming that some heat is lost to the surroundings so that the final mixture is liquid and the final pressure and temperature are the same as those of condensed vapor from the last effect), and the mixture is transferred out of the evaporator through the ‘Condensed Vapor’ port. The vapor of the last effect leaves the evaporator through the ‘Vapor’ port. Finally, the final concentrated solution coming out of the last effect (if forward feed flow arrangement is used) or the first effect (if backward feed flow arrangement is used) leaves the evaporator through the ‘Liquor’ port.
To indicate that the equipment contains two or more effects, the ‘Evaporation Data (Per Effect)’ table shown in the Effects tab of this operation’s data dialog must contain two or more rows (see Multi-Effect Evaporation: Effects Tab).
To indicate that no vapor recompression is employed, ‘None’ must be selected in the Vapor Recompression Options that are available in the Oper. Conds Tab of the same dialog (see Multi-Effect Evaporation: Oper. Conds Tab).
If the previous multi-effect evaporation is used, and vapor recompression is also employed, then a fraction of the vapor produced by a chosen effect (if thermal vapor recompression is used) or by the last effect (if mechanical vapor recompression is used) may be recovered, recompressed and used as heating fluid in the heating space of the first effect, where it becomes condensed vapor. As previously, the individual condensed vapors from all effects are mixed together non-adiabatically, and the mixture is transferred out of the evaporator through the ‘Condensed Vapor’ port. The fraction of vapor produced by the last effect that is not recompressed leaves the evaporator through the ‘Vapor’ port. Finally, the final concentrated solution leaves the evaporator through the ‘Liquor’ port.
In order to model vapor recompression, either ‘Mechanical Vapor Recompression’ or ‘Thermal Vapor Recompression’ must be selected in the Vapor Recompression Options that are available in the Oper. Conds Tab of the operation’s data dialog (see Multi-Effect Evaporation: Oper. Conds Tab).
The main model inputs (including inputs which may not be set by user directly but may be calculated based on other inputs and/or model assumptions) are:
Oper. Conds Tab:
● The specification of one or more components as ‘Volatile’.
● The Evaporation % for each volatile component.
● The choice of Feed Flow Arrangement (Forward or Backward).
● The choice of Vapor Recompression Option (None, MVR or TVR).
Heating tab (all options):
● The Supply Temperature of Heating Agent. Depending on the choice of vapor recompression option, this may correspond to: (a) the inlet temperature of heating agent in the heating space of the first effect (if no vapor recompression is used); (b) the temperature of “make-up” heating agent before mixing with recompressed vapor and/or desuperheating agent (for MVR); or (c) the inlet temperature of “motive” heating agent in the steam-jet ejector (for TVR).
● The Return Temperature of Heating Agent. Depending on the choice of vapor recompression option, this may correspond to: (a) the outlet temperature of heating agent from the heating space of the first effect (if no vapor recompression is used); (b) the outlet temperature of the heating fluid (mixture of recompressed vapor, desuperheating agent and heating agent) from the heating space of the first effect (for MVR); or (c) the outlet temperature of heating fluid (mixture of recompressed vapor and heating agent) from the heating space of the first effect (for TVR).
● The Mass-to-Energy Factor of the Heating Agent. This is the specific heat source of the heating agent between supply and return points. Depending on the choice of vapor recompression option, this may correspond to: (a) the specific heat source due to heat transfer to the solution in the heating space of the first effect (if no vapor recompression is used); (b) the net sum of the specific enthalpy change due to mixing with recompressed vapor and (optionally) desuperheating agent and the specific heat source due to heat transfer to the solution in the heating space of the first effect (for MVR); or (c) the net sum of the specific heat source due to mixing with vapor in the steam-jet ejector and the specific heat source due to heat transfer to the solution in the heating space of the first effect (for TVR).
● The estimate of hot-side stream temperature in the first effect (Condensing Temperature of Heating Fluid in First Effect).
Heating tab (for MVR option only):
● The percentage of vapor produced by the last effect that is recovered and recompressed (Recompressed %) (for MVR).
● The specific enthalpy change of vapor by compression (Compression Work) (for MVR).
● The Supply Temperature of Desuperheating Agent (for MVR). This corresponds to the temperature of the desuperheating agent before it is mixed with recompressed vapor.
● The Return Temperature of Desuperheating Agent (for MVR). This correspond to the outlet temperature of heating fluid (mixture of recompressed vapor, desuperheating agent and heating agent) from the heating space of the first effect.
● The Mass-to-Energy Factor of Desuperheating Agent (for MVR). This is the specific heat sink of the desperheating agent between supply and return points. It the net sum of the specific heat sink due to mixing with recompressed vapor and (optionally) heating agent and the specific heat source due to heat transfer to the solution in the heating space of the first effect.
Heating tab (for TVR option only):
● The choice of the effect from which vapor is drawn for recompression (“From Effect”) (for TVR).
● The Entrainment Ratio (for TVR).
Effects tab:
● The temperature of concentrated liquor in the last effect (based on the flow of vapor) (Liquor Temp. in Last Effect).
● The enthalpy of the dilute solution that is fed to the evaporator (Feed Enthalpy).
● The enthalpy of concentrated solution for each effect (Liquor Enthalpy).
● The enthalpy of vapor produced by each effect (Vapor Enthalpy).
● The specific heat source of the hot-side stream in each effect (Specific Heat Duty).
● The overall heat transfer coefficient for each effect (Heat Transfer Coefficient).
● The temperature difference between the hot-side stream and the cold-side stream for each effect (Mean Temp. Difference).
● The boiling point elevation for each effect (BPE).
The main model outputs are:
● The Heating Agent Flow (see Heating tab).
● The Desuperheating Agent Flow (see Heating tab) (for MVR).
● The Heat Transfer Area for each effect (see Effects tab).
In the general case of a multi-effect evaporator consisting of n effects, the overall total and component material balances have the form:
|
|
|
|
where:
● F is the mass flow rate of the initial dilute solution (feed).
● L is the mass flow rate of the final concentrated solution (liquor).
● Vtot is the total mass evaporation rate (evaporation capacity).
● xF,j is the mass fraction of component j in the initial dilute solution.
● xL,j is the mass fraction of component j in the final concentrated solution.
● yVtot,j is the fraction of Vtot corresponding to component j.
The (total) evaporation % of component j (ej) is defined as the percent ratio of the corresponding total mass evaporation rate (VtotyVtot,j) to the corresponding mass flow rate in the initial dilute solution (FxF,j):
|
|
The (total) relative mass evaporation rate of component j (rj) is defined as the ratio of the corresponding evaporation % (ej) to the maximum evaporation % among all evaporating components (emax):
|
|
The following specification options are available for solving the overall total and component material balances:
a) Set Final Concentration Of Key Component
b) Set Final Mass Fraction Of Key Component
c) Set Evaporation % For Each Volatile Component
If option (a) is selected, the final concentration of a key component is specified along with the relative mass evaporation rate for each component that is set as volatile. The temperature, density and final mass fraction of the final concentrated solution are determined by solving the system of mass and energy balances for this operation (see below). Then, the evaporation % for the key component (ek) is calculated based on eq. (A.265) and eq. (A.266); the maximum evaporation % of all volatile components (emax) is calculated as rkek based on eq. (A.267); the evaporation % for each of the other volatile components is calculated based on eq. (A.267).
If option (b) is selected, the final mass fraction of a key component is specified along with the relative mass evaporation rate for each component that is set as volatile. Same as before, the evaporation % for the key component (ek) is calculated based on eq. (A.265) and eq. (A.266); the maximum evaporation % of all volatile components (emax) is calculated as rkek based on eq. (A.267); the evaporation % for each of the other volatile components is calculated based on eq. (A.267).
If option (c) is selected, the evaporation % for each volatile component is specified. The maximum of all specified evaporation % is determined and the relative mass evaporation rate for each component that is set as volatile is calculated based on eq. (A.267).
After the evaporation % for each volatile component is determined, the eq. (A.264) and eq. (A.265) are solved in order to determine the total mass flow rate (L) and composition (xL,j) of the final concentrated solution and the evaporation capacity (Vtot).
Consider a multi-effect evaporator consisting of n effects (i=1, 2, ..., n). The mass and energy balances for effect i have the form:
|
|
|
|
where:
● Fi is the mass flow rate of the feed in effect i.
● Li is the mass flow rate of liquor produced in effect i.
● Vi is the mass flow rate of vapor produced in effect i.
● Qi is the heat transfer rate from the heating fluid to the solution in effect i.
● Vh,i is the mass flow rate of heating fluid in the heating space of effect i.
● ΔHh,i is the specific enthalpy change of heating fluid in the heating space of effect i.
● HhV,i is the specific inlet enthalpy of heating fluid in the heating space of effect i.
● HhL,i is the specific outlet enthalpy of heating fluid from the heating space of effect i.
● HV,i is the specific enthalpy of vapor produced in effect i.
● HL,i is the specific enthalpy of liquor produced in effect i.
● HF,i is the specific enthalpy of the feed in effect i.
A schematic of the flows of heating fluid, feed, vapor and liquor in a multi-effect evaporator for forward feed flow arrangement is shown below. The flow of vapor is from left to right and so is the order in which the effects are numbered. For forward feed flow arrangement, the feed in the first effect corresponds to the initial dilute solution (F1 = F, HF,1 = HF). The feed in the second, third, and each subsequent effect, corresponds to the concentrated solution produced by each preceding effect (Fi = Li-1, HF,i = HL,i-1, i= 2, 3, ..., n). The flow of heating fluid in the first effect (Vh,1) corresponds to the flow of heating agent (S). The flow of heating fluid in the second, third, and each subsequent effect, corresponds to the flow of vapor produced by each preceding effect (Vh,i = Vi-1, i= 2, 3, ..., n). The specific heat duty of heating fluid in the first effect (-ΔHh,1 = HhV,1 - HhL,1) corresponds to the mass-to-energy factor of the selected heating agent (-ΔHs). The specific inlet enthalpy of heating fluid to the heating space of the second, third, and each subsequent effect, corresponds to the specific enthalpy of vapor produced by each preceding effect (HhV,i = HV,i-1, i= 2, 3, ..., n). The specific heat duty of heating fluid in the second, third, and each subsequent effect, corresponds to the latent heat of condensation of the corresponding fluid in the heating space of the corresponding effect (-ΔHh,i = HhV,i - HhL,i = λi, i= 2, 3, ..., n).
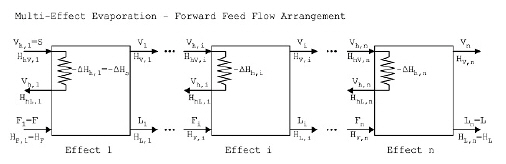
A schematic of the flows of heating fluid, feed, vapor and liquor in a multi-effect evaporator for backward feed flow arrangement is shown below. The flows of heating fluid and vapor are the same as those for forward feed flow arrangement. For backward feed flow arrangement, the feed in the last effect (n) corresponds to the initial dilute solution (Fn = F, HF,n = HF). The feed in effect n-1, n-2, and in each preceding effect i (i=n-1, n-2, ..., 2, 1), corresponds to the concentrated solution produced by each subsequent effect (Fi = Li+1, HF,i = HL,i+1, i= 1, 2, ..., n-1).
A schematic of the flow diagram for multi-effect evaporation with mechanical vapor recompression is shown below. Differences with plain multi-effect evaporation are marked in red. In mechanical vapor recompression, a fraction (r) of vapor produced by the last effect (Vn) is compressed in a mechanical compressor. Optionally, the recompressed vapor may be mixed with desuperheating agent (D). If the heat supplied by this mixture is less than the heat required to boil the solution in the first effect, then a “make-up” heating agent (S) is added to the mixture in order to supply the extra heat.
For MVR, the specific enthalpy change of vapor by mechanical compression is calculated as:
|
|
where:
● Wc is the specific enthalpy change of vapor by mechanical compression.
● Pin is the pressure of vapor at compressor inlet.
● ρin is the density of vapor at compressor inlet.
● εi is the efficiency of isentropic mechanical compression.
● kc is the specific heat ratio, which can be estimated as 1/(1-R/cp), where R is the universal gas constant and cp is the molar specific heat capacity of vapor at the inlet of the compressor.
● Pout is the pressure of vapor at compressor outlet.
The compressor power is calculated as:
|
|
eq. (A.271) |
where:
Vn is the flow of vapor produced by the last effect (n).
r is the fraction of vapor produced by the last effect that is sent to the compressor.
fc is the percentage of other efficiency losses in the mechanical compressor than those corresponding to the isentropic efficiency.
If MVR is employed, the total mass flow rate of heating fluid in the heating space of the first effect is given by:
|
|
where:
● S is the mass flow rate of heating agent.
● D is the mass flow rate of desuperheating agent.
● r is the fraction of vapor produced by the last effect that is recovered and recompressed.
By applying eq. (A.269) to the first effect, the following equation is derived for the heat transfer rate in the first effect:
|
|
It is assumed that the heating agent, the recompressed vapor, and the desuperheating agent, all have the same specific enthalpy at the outlet of the heating space of the first effect. Based on this assumption, the heat transfer rate in the first effect for MVR can also be expressed as:
|
|
where:
● ΔHS is the specific enthalpy change of heating agent between the corresponding supply point (HS) and the heating space outlet of first effect (HhL,1); consequently, -ΔHS is equal to the mass-to-energy factor of the heating agent.
● ΔHD is the specific enthalpy change of desuperheating agent between the corresponding supply point (HD) and the heating space outlet of the first effect (HhL,1); it is equal to the mass-to-energy factor of the desuperheating agent.
By combining eq. (A.272), eq. (A.273) and eq. (A.274), the following equation can be derived for the specific heat transfer rate (or specific heat duty) of the first effect (-ΔHh,1):
|
|
eq. (A.275) |
If no desuperheating agent is used, then the flow of desuperheating agent (D) is zero. In that case, the specific heat transfer rate in the first effect is calculated by the program based on the above equation.
On the other hand, if a desuperheating is used, then the following possibilities exist for the specific heat duty of the first effect:
● If the option Same Properties As Vapor is not checked, then the specific heat duty of the first effect must be set by user.
● If the option Same Properties As Vapor is checked, and the option Calculated for Steam Using Steam Calculator (see Effects tab) for the properties of vapor is also checked, then the specific heat duty of the first effect is calculated based on the built-in steam calculator as the latent heat of vaporization of steam at the condensing temperature of heating fluid in the first effect.
● If the option Same Properties As Vapor is checked, and the option Calculated for Steam Using Steam Calculator (see above) is not checked, then the specific heat duty of the first effect is calculated as the latent heat of vaporization of recompressed vapor at the condensing temperature of heating fluid in the first effect.
If a desuperheating agent is used, the program uses the above equation to calculate the flow of desuperheating agent.
A schematic of the flows in case of multi-effect evaporation with thermal vapor recompression is shown below. Differences with plain multi-effect evaporation are marked in red.
In thermal vapor recompression, a fraction (r) of vapor produced by one of the effects (usually, the first) is drawn from the vapor outlet of that effect and is entrained in a steam-jet ejector, where it is mixed with “motive” heating agent in order to become recompressed. The resulting mixture of heating agent and recompressed vapor is then fed to the heating space of the first effect. Therefore, if TVR is employed, the total mass flow rate of heating fluid in the heating space of the first effect is given by:
|
|
where:
● k is the selected effect from which vapor is drawn and recompressed in TVR.
● r is the fraction of vapor produced by effect k that is recovered and recompressed.
● ER is the entrainment ratio (i.e., the ratio of mass flow rate of entrained vapor to mass flow rate of heating agent) in the steam-jet ejector.
As in the case of MVR, it is assumed that the heating agent and recompressed vapor have the same specific enthalpy at the outlet of the heating space of the first effect. Based on this assumption, the heat transfer rate in the first effect for TVR can be expressed as:
|
|
By combining eq. (A.273), eq. (A.276) and eq. (A.277), the following equation can be derived for the specific heat transfer rate of the first effect (-ΔHh,1):
|
|
eq. (A.278) |
If TVR is used, the specific heat transfer rate of the first effect is calculated based on the above equation.
In addition to eq. (A.268) and eq. (A.269), the program solves the component mass balances for effect i, which have the following form:
|
|
where:
● xF,j,i is the mass fraction of component j in the feed of effect i.
● xL,j,i is the mass fraction of component j in the concentrated solution produced by effect i.
● yV,j,i is the mass fraction of component j in the vapor produced by effect i.
In the absence of phase equilibrium data, it is assumed that the relative component evaporation fractions (yj/yk) for effect i are the same as the respective overall relative component evaporation fractions:
|
|
Based on this assumption, an approximate composition is initially calculated for the vapor phase in each effect. Subsequently, the corresponding composition of liquor for each effect is calculated based on the component mass balances for each effect according to eq. (A.279).
If no vapor recompression is employed, the system of M&E balance equations eq. (A.268) and eq. (A.269) is solved and the mass flow rates of heating agent (S) and vapor per effect (Vi) are calculated based on inputs of mass-to-energy factor of the heating agent (-ΔHS), feed specific enthalpy (HF) (optional), liquor specific enthalpy per effect (HL,i) (optional), vapor specific enthalpy per effect (HV,i) (optional), and specific heat duty per effect (-ΔHh,i) (optional).
If MVR is employed, the system of M&E balance equations eq. (A.268), eq. (A.269), eq. (A.270), eq. (A.272) and eq. (A.274) is solved and the mass flow rates of heating agent (S), vapor per effect (Vi), and (optionally) desuperheating agent (D) are calculated based on inputs of isentropic efficiency (εi), specific heat ratio (kc) (optional), specific outlet enthalpy of heating fluid in first effect (HhL,1) (optional), pressure in heating space of first effect (optional), and specific heat duty in first effect (-ΔHh,1) (optional) (in addition to the inputs required for plain multi-effect evaporation).
If TVR is employed, the system of M&E balance equations eq. (A.268), eq. (A.269), eq. (A.276) and eq. (A.277) is solved and the mass flow rates of heating agent (S) and vapor per effect (Vi) are calculated based on inputs of entrainment ratio (ER), choice of effect from which vapor is drawn and sent for recompression (k), specific outlet enthalpy of heating fluid in first effect (HhL,1) (optional), and pressure in heating space of first effect (optional) (in addition to the inputs required for plain multi-effect evaporation).
If there is no vapor recompression, or if there is TVR, the evaporation economy is calculated based on the following equation:
|
|
eq. (A.281) |
For MVR, the evaporation economy is calculated based on the following equation:
|
|
eq. (A.282) |
In this equation, a fictitious heating agent flow is calculated by dividing the compressor power by the mass-to-energy factor of the heating agent (-ΔHS). This is added to the actual heating agent flow (S) in the denominator in order to account for the operating cost of compression in the overall economy of the evaporation system.
The heat exchanger design equation is used to calculate the heat transfer area per effect:
|
|
where:
● Ui is heat transfer coefficient in effect i.
● Ai is heat transfer area of effect i.
● ΔTi is the mean temperature difference between the hot stream (heating fluid) and the cold stream (solution) in effect i.
For preliminary design, it is customary to approximate the true mean temperature difference as:
|
|
where:
● Tc,i is the condensing temperature of heating fluid in the heating space of effect i.
● TL,i is the boiling point of liquor in effect i.
For a single effect, the above equation is used to estimate ΔT1 based on Tc,1 and TL,1. For two or more effects, the above equation is used to estimate TL,i based on Tc,i and ΔTi.
The boiling point elevation for each effect is defined as:
|
|
where:
● BPEi is the boiling point elevation in effect i.
● TV,i is the boiling point of vapor in effect i.
The above equation is used to estimate TV,i based on TL,i and BPEi.
If N effects are used (N>1), the values of Tc,1 and TL,N are specified. The values of Tc,i (i= 2, 3, ..., N) are estimated based on the assumption that the pressure in the heating space of the second, third, and each subsequent effect, is the same as the pressure of the vapor phase produced by each preceding effect. Thereby, the condensing temperature of heating fluid in the second, third, and each subsequent effect, is assumed equal to the vapor temperature in each preceding effect (Tc,i = TV,i-1, i= 2, 3, ..., N).
The following options are available for determining the values of ΔTi (i=1, 2, ..., N) if two or more effects are used:
a) Set by User
b) Calculated Based on Equal Heat Transfer Areas
If option (a) is selected, the values of ΔTi (i=1, 2, ..., N) are set by the user. The heat transfer area for each effect is then calculated based on eq. (A.283). Also, the mean heat transfer area is calculated as the average value of the heat transfer areas of all effects.
If option (b) is selected, initial estimates of ΔTi (i=1, 2, ..., N) are first calculated based on the following expression:
|
|
The above expression is derived by applying eq. (A.283) to all effects and assuming that the heat flux (Q/A) is the same for all effects. Subsequently, initial estimates of the heat transfer area for each effect are calculated based on eq. (A.283) and an initial estimate of mean heat transfer area is computed based on the those estimates. If the heat transfer areas of two or more effects are not equal within a certain degree of tolerance, the program will do the following:
1. Calculate new values for the mean temperature difference per effect by adjusting the old ones using suitable weights.
2. Calculate new values for the liquor and vapor boiling points per effect, based on eq. (A.284) and eq. (A.285), respectively.
3. Calculate new values for the vapor pressure per effect (see below).
4. Calculate new values for the specific enthalpies of liquor and vapor per effect (if these are not set by user).
5. Solve the system of M&E balance equations (described previously) in order to calculate new values for the mass flow rates of heating agent, vapor per effect, recompressed vapor (if used) and desuperheating agent (if used).
6. Calculate new values for the heat transfer area per effect based on eq. (A.283) and, based on those values, calculate a new value for the mean heat transfer area.
The above steps are repeated until the relative difference between the heat transfer area of each effect and the mean heat transfer area is lower than or equal to the built-in relative error tolerance (10-11). For each effect, the relative difference between the heat transfer area of that effect and the mean heat transfer area is calculated as 1 - (heat transfer area) / (mean heat transfer area).
To correctly determine the boiling point of the concentrated solution (liquor) for each effect, it may be important to consider its boiling point elevation (BPE). If this is a weak function of concentration, you may set the BPE for each effect equal to zero. If, however, the BPE per effect is significant, then you can specify user-defined values for the BPE for each effect. The BPE of a solution as a function of concentration can be found from tables, charts (such as the Duehring plots) or correlations that are available in the literature.
To correctly determine the enthalpy of the initial dilute solution (feed) and of the concentrated liquor for each effect, it may be important to account for the heats of dilution of those solutions. If these are not significant, you may check the option Neglect Heat of Dilution. If this option is checked, then the specific enthalpy of each solution (feed, liquor per effect) will be computed based on the standard approach used in the program for calculating the enthalpy of a stream (i.e., based on the corresponding temperature, composition and pure component specific heat capacities), which does not account for heat of dilution. However, if the heat of dilution is significant for the solution considered, you may un-check the above option and specify user-defined values for the feed enthalpy correction and the relative liquor enthalpy for each effect. The feed enthalpy correction (ΔHcorr,F) is defined as the difference between the actual value of specific enthalpy of the feed (HF) and the standard value of feed specific enthalpy calculated by the program (H*F):
|
|
eq. (A.287) |
where:
● H*F is the standard value of feed specific enthalpy calculated by the program (in kJ/kg).
● ΔHcorr,F is the feed enthalpy correction (in kJ/kg).
The relative liquor enthalpy for effect i (ΔHcorr,L,i) is defined as the difference between the actual value of specific enthalpy of liquor in that effect (HL,i) and the standard value of feed specific enthalpy calculated by the program (H*F):
|
|
eq. (A.288) |
where ΔHcorr,L,i is the relative liquor enthalpy for effect i (in kJ/kg).
The liquor temperature per effect is assumed equal to the corresponding boiling point. It is calculated based on eq. (A.284).
For each effect, the vapor temperature is assumed equal to the liquor temperature.
If the properties of vapor (per effect) are not Calculated for Steam Using Steam Calculator (see below), the pressure of vapor in each effect is calculated based on the following expression, which is derived by combining the ideal gas laws of Dalton and Raoult:
|
|
where:
● pi is the pressure in the vapor space of effect i.
● pi,j is the partial pressure of volatile component j in vapor space of effect i.
● xF,j,i is the mole fraction of volatile component j in the feed of effect i.
● pj0 is the vapor pressure of volatile component j.
The vapor pressure of a pure component is calculated as a function of temperature based on the Antoine Equation for that component (see the pure component properties dialog).
If the properties of vapor (per effect) are not Calculated for Steam Using Steam Calculator (see below), then two options are available for determining the specific enthalpy of vapor for each effect:
a) Set by User
b) Calculated
If option (b) is selected, then the specific enthalpy of vapor for each effect is calculated based on the standard approach used in the program for calculating the enthalpy of a stream (i.e., based on the corresponding temperature, composition and pure component specific heat capacities).
If option (a) is selected, you must specify user-defined values for the relative vapor enthalpy per effect. The relative vapor enthalpy for effect i (ΔHcorr,V,i) is defined as the difference between the actual value of specific enthalpy of vapor in that effect (HV,i) and the standard value of feed specific enthalpy calculated by the program (H*F):
|
|
eq. (A.290) |
where ΔHcorr,V,i is the relative vapor enthalpy for effect i (in kJ/kg).
If the vapor phase consists mainly of steam, and you wish to ignore the effect of concentration, the properties of vapor (per effect) can be Calculated for Steam Using Steam Calculator by checking the corresponding option. If this option is checked, it is assumed that the properties of vapor (per effect) are essentially those of steam (calculated based on the built-in steam calculator). In that case:
● The pressure of vapor for each effect is set equal to the pressure of saturated steam at the corresponding vapor temperature (calculated based on the built-in steam calculator).
● The specific enthalpy of vapor for each effect is set equal to the specific enthalpy of steam at the corresponding temperature and pressure (calculated based on the built-in steam calculator).
The heating fluid in the heating space of the first effect may be a mixture of heating agent, recompressed vapor (if TVR or MVR are used) and desuperheating agent (if MVR and desuperheating are used).
For simplicity, it is assumed that the heating fluid in the first effect has the same composition, and thereby, thermodynamic properties as the heating agent (e.g., they have the same condensing temperature for a particular pressure and the same specific enthalpy for a particular temperature and pressure).
Based on this assumption, the condensing temperature of heating fluid in the heating space of the first effect is assumed equal to the condensing temperature of heating agent in the first effect. If the supply and return temperatures of the heating agent are the same, then the condensing temperature of the heating fluid in the first effect is assumed equal to the return temperature of the heating agent. If the supply and return temperatures of the heating agent are the different, then the condensing temperature of the heating fluid in the first effect can be set by the user. In this case, it must be within the range defined by the supply and return temperatures of the heating agent.
Based on the same assumption, the outlet temperature of heating fluid from the heating space of the first effect is assumed equal to the return temperature of the heating agent. (If MVR and desuperheating are used, then the return temperature of the desuperheating agent must also match this value).
Another simplification is possible if vapor recompression is used, and the heating fluid in the first effect consists mainly of recompressed vapor. In this case, the heating fluid in the first effect may be assumed to have the Same Properties As Vapor by checking the corresponding option. If this option is checked, then the heating fluid in the first effect and the recompressed vapor are assumed to have the same composition, and thereby, thermodynamic properties (e.g., they have the same pressure at the condensing temperature, and the same specific enthalpy with respect to temperature and pressure).
The pressure of heating fluid in the first effect is determined as follows:
● If the option Same Properties As Vapor is not checked, then it must be set by user.
● If the option Same Properties As Vapor is checked, and the option Calculated for Steam Using Steam Calculator (see above) is also checked, then it is set equal to the pressure of saturated steam corresponding to the condensing temperature of heating fluid in first effect (calculated based on the built-in steam calculator).
● If the option Same Properties As Vapor is checked, and the option Calculated for Steam Using Steam Calculator (see above) is not checked, then it is calculated based on eq. (A.289).
The specific outlet enthalpy of heating fluid from the heating space of the first effect is determined as follows:
● If the option Same Properties As Vapor is not checked, then it must be set by user.
● If the option Same Properties As Vapor is checked, and the option Calculated for Steam Using Steam Calculator (see above) is also checked, then it is set equal to the specific enthalpy of water corresponding to the temperature and pressure of heating fluid at the outlet of the heating space of the first effect (calculated based on the built-in steam calculator).
● If the option Same Properties As Vapor is checked, and the option Calculated for Steam Using Steam Calculator (see above) is not checked, then it is calculated as the enthalpy of recompressed vapor corresponding to the temperature and pressure of heating fluid at the outlet of the heating space.
The specific heat duty for the first effect is determined as follows:
● If no vapor recompression is employed, it is set equal to the mass-to-energy factor of the heating agent.
● If MVR is employed, and a desuperheating is used, and the option Same Properties As Vapor is not checked, then it must be set by user.
● If MVR is employed, and a desuperheating is used, and the option Same Properties As Vapor is checked, and the option Calculated for Steam Using Steam Calculator (see above) is also checked, then it is set equal to the latent heat of vaporization of steam at the condensing temperature of heating fluid in the first effect (calculated based on the built-in steam calculator).
● If MVR is employed, and a desuperheating is used, and the option Same Properties As Vapor is checked, and the option Calculated for Steam Using Steam Calculator (see above) is not checked, then it is calculated as the latent heat of vaporization of recompressed vapor at the condensing temperature of heating fluid in the first effect.
● In any other case, it is calculated as Q1/Vh,1 according to eq. (A.273).
The specific inlet enthalpy of heating fluid in the first effect is calculated as the sum of the corresponding specific outlet enthalpy and the corresponding specific heat duty.
The inlet temperature, pressure and specific enthalpy of heating fluid in the heating space of the second, third, and each subsequent effect, are assumed equal to the corresponding temperature, pressure and specific enthalpy of vapor produced by each preceding effect. Since the vapor temperature is equal to the condensing temperature for each effect, the condensing and outlet temperatures of heating fluid in the second, third, and each subsequent effect, are assumed equal to the corresponding inlet temperature of heating fluid in that effect.
If the option Calculated for Steam Using Steam Calculator (see above) is not checked, two options are available for determining the specific heat duty for the second, third, and each subsequent effect:
a) Set by User
b) Calculated
If option (a) is selected, then it is calculated baed on eq. (A.269). If option (b) is selected, then it is calculated as the difference between inlet and outlet enthalpy, where the outlet enthalpy is calculated as the enthalpy of condensed vapor at the corresponding temperature.
If the option Calculated for Steam Using Steam Calculator (see above) is checked, then the specific heat duty for the second, third, and each subsequent effect is calculated as the difference between inlet and outlet enthalpy, where the outlet enthalpy is set equal to the enthalpy of saturated water at the corresponding pressure (calculated based on the built-in steam calculator).
1. McCabe W. L., J. C. Smith and P. Harriott (1993). Unit Operations of Chemical Engineering, McGraw-Hill.
2. Kern D. Q (1965). Process Heat Transfer, McGraw-Hill.
3. Coulson J. M. and J. F. Richardson, (1978). Chemical Engineering, 2, Pergamon Press.
● The feed stream must carry material of non-zero liquid/solid flow.
● The condensing temperature of the heating fluid in the first effect must be higher than the temperature of the feed stream; also, it must be within the range defined by the supply and return temperatures of the heating agent.
● If you set the final concentration (or mass fraction) of a key component, that component must be present in the feed stream. If that component is non-volatile, the final concentration (or mass fraction) must be greater than the corresponding concentration (or mass fraction) in the feed stream. Also, the relative mass evaporation rate must be greater than zero for at least one that exists in the feed stream and is set as volatile.
● If the evaporation % for each volatile component is set, then the evaporation % must be greater than zero for at least one component that exists in the feed stream and is set as volatile.
● In multi-effect evaporation, the composition and enthalpy of intermediate vapor and liquid streams are approximately determined by assuming that the relative component evaporation fractions are equal to the corresponding relative total evaporation fractions for all effects.
● In multi-effect evaporation, the pressure in the heating space of the second, third, and each subsequently effect, is assumed equal to the corresponding pressure of vapor produced by each preceding effect.
● If vapor recompression is used, the heating fluid in the first effect is assumed to have the same composition, and thereby, thermodynamic properties as the heating agent.
The interface of this operation has the following tabs:
● Oper. Cond’s, see Multi-Effect Evaporation: Oper. Conds Tab
● Heating, see Multi-Effect Evaporation: Heating Tab, Multi-Effect Evaporation: Heating Tab (MVR), or Multi-Effect Evaporation: Heating Tab (TVR)
● Effects, see Multi-Effect Evaporation: Effects Tab
● Power, see Multi-Effect Evaporation: Power Tab, or Multi-Effect Evaporation: Power Tab (MVR)
● Labor, etc, see Operations Dialog: Labor etc. Tab
● Description, see Operations Dialog: Description Tab
● Batch Sheet, see Operations Dialog: Batch Sheet Tab
● Scheduling, see Operations Dialog: Scheduling Tab
