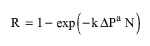
eq. (A.153)
High-pressure homogenization is used in the food industries to homogenize milk, various creams, and other products. The same equipment, operating under higher-pressure drops, is used in the biochemical industries to disrupt (break-open) microorganisms and release intracellular products. For cell disruption, the cell slurry is pumped through a narrow ring gap at pressures up to 1200 bar (depending on the microorganism and the operating mode). The large pressure drop creates high liquid velocities that cause cavitation and turbulence. The resulting fluid oscillation and high shear forces are the primary causes of cell disruption. The disrupted cells release the intracellular protein but because of the high shear rate a fraction of the protein is denatured. To increase the extent of cell disruption, the broth typically passes several times through the disruption unit. The multiple passes also help reduce the viscosity of the suspension by fragmenting the released nucleic acids.
● High Pressure Homogenization Procedure
Cell disruption is described by an empirical model, which relates the fraction of cells disrupted (R) to the pressure drop (ΔP) across the valve and the number of discrete passes (N) (Hetherington et al., 1971):
|
|
eq. (A.153) |
where a is a constant (cell- and equipment-dependent) and k is a release rate constant (cell-, equipment-, and temperature-dependent). Constant a for most microorganisms is approximately equal to 2.9. The fraction of the released intracellular proteins that are denatured (D) is given by the following equation:
|
|
eq. (A.154) |
The parameter φ usually has values between 0.0 and 0.3.
To account for situations where the values of a, k, and φ are not known but instead actual experimental data are available, the user has the option to specify the release and denaturation fractions.
The user may specify a reaction stoichiometry for the homogenization step representing the disruption of biomass. If, for instance, the product of fermentation is an intracellular protein that forms inclusion bodies, the homogenization reaction may be:
|
|
with a stoichiometry which is also given above. Note that this is a mass stoichiometry and the sum of all coefficients must be equal to zero to have conservation of mass.
In this case, simply specify the pressure drop through the valve so that the model can calculate the power requirement. There is no need to specify a reaction stoichiometry since no material transformation takes place.
The electric power required to pump the fluid through the valve is estimated by the following equation:
|
|
eq. (A.156) |
where m is the mass flowrate of the fluid through the valve, ρ is the density of the fluid, and η is the overall efficiency of the pumping system. It is assumed that all pumping power eventually dissipates into heat that contributes to the cooling or heating requirement.
1. Hetherington, P. J. et al. (1978). Release of Proteins from Baker's Yeast (Saccharomyces cerevisiae) by Disruption in an Industrial Homogenizer, Trans. Instn. Chem. Engrs, 49.
2. Kula, Maria-Regina and Horst Schutte (1987). Purification of Proteins and the Disruption of Microbial Cells. Biotechnology Progress, March, 3, 1, 31-42.
The interface of this operation has the following tabs:
● Oper. Cond’s, see High Pressure Homogenization: Oper. Conds Tab
● Mat. Balance, see High Pressure Homogenization: Mat. Balance Tab
● Labor, etc, see Operations Dialog: Labor etc. Tab
● Description, see Operations Dialog: Description Tab
● Batch Sheet, see Operations Dialog: Batch Sheet Tab
● Scheduling, see Operations Dialog: Scheduling Tab