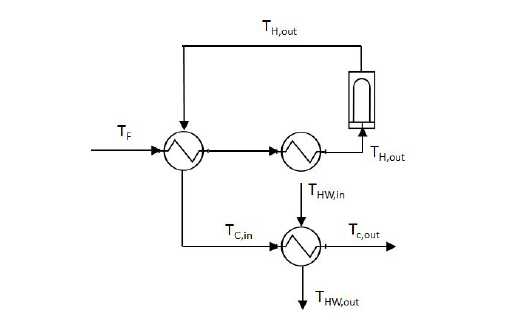
This model calculates the sizing variables of a pasteurizer comprising a holding tube and three individual heat exchangers namely, a heater, a cooler and (optionally) a regenerator. It also accounts for the microorganism degradation and food component inactivation during the pasteurization process.

In design mode, the model calculates the individual heat transfer areas of the pasteurizer’s heater, cooler and regenerator sections assuming countercurrent flow conditions for all heat exhangers. The heat transfer area, Ax, is calculated by the following equation
|
|
eq. (A.339) |
where:
● x stands for the heater, cooler or regenerator
● Qx denotes the thermal load of the heat exchanger (J/s)
● Ux is the overall heat transfer coefficient (W m-2 K-1)
● ΔΤM,x is a mean temperature difference (K), calculated by
|
|
eq. (A.340) |
● :
where:
● TF temperature of the pasteurizer’s feed stream (K)
● TH,in is the temperature of the stream entering the heater (regenerator cold stream exit temperature) (K)
● TH,out is the temperature of the stream leaving the heater (pasteurization temperature) (K)
● TC,in is the temperature of the stream entering the cooler (regenerator hot stream exit temperature) (K)
● TC,out is the temperature of the stream leaving the cooler (final exit temperature) (K)
● THA,in, THA,out and TCA,in, TCA,out denote the inlet and outlet temperatures of the heating and cooling agent streams, respectively (K).
Notice that while a logarithmic mean temperature difference is employed for the heater and the cooler, an arithmetic mean is employed in the case of the regenerator. This is a necessary modification required by the fact that the same liquid, at the same flowrate, is heated and cooled in the regenerator so the logarithmic mean temperature difference is “forced” to infinity.
The regenerator efficiency defined by:
|
|
eq. (A.341) |
expresses the percentage of the temperature increase that is achieved by the regenerator w.r.t the overall required temperature increase (i.e., in order to reach the desired pasteurization temperaure). According to the literature, regeneration efficiencies of up to 94-95 % can be achieved in efficient modern pasteurization plants.
In design mode the diameter of the of the holding tube (in m) is calculated by:
|
|
eq. (A.342) |
where:
● Q is the volumetric throughput (m3/s)
● ρ is the density of the pasteurized liquid (kg/m3)
● μ is its viscosity (Pa s)
● Re is the Reynolds number that corresponds to the flow in the holding tube
The volume of the holding tube (in m3) is calculated by the following equation:
|
|
eq. (A.343) |
where:
● τ is the residence time in the holding tube (s)
● η is a holding tube efficiency
The latter is used in order to “enforce” that even the fastest liquid molecule (i.e., with respect to the average velocity in the tube) is sufficiently pasteurized.
Finally, the length of the holding tube (in m) is calculated by:
|
|
eq. (A.344) |
and the average velocity of the pasteurized liquid that flows inside it (in m/s) is given by:
|
|
eq. (A.345) |
The death of microorganisms during the residence of a liquid within the holding tube of a pasteurizer is commonly represented by the following equation (Wang et al, 1979):
|
|
eq. (A.346) |
where:
● N is the number concentration of viable cells (# / L)
● k is the specific death rate constant (s-1)
● t is the process time (s).
By integration of the above equation under the constant specific death rate assumption (i.e., k is not a function of time) one gets:
|
|
where N0 in the initial number concentration of viable microorganism cells. By changing the logarithmic base, the above equation can be transformed into:
|
|
eq. (A.348) |
The quantity D, commonly known as the decimal reduction time, expresses the time required at a given temperature in order to achieve a 90% reduction in the number of viable cells of a population (i.e., one log cycle). The temperature dependence of D is assumed by the model to follow the Canners’ (or constant z) model expressed by:
|
|
eq. (A.349) |
where:
● z is the thermal resistance factor (K)
● D(T) is the decimal reduction time at the pasteurization temperature T (s)
● D(TR) is the decimal reduction time at a reference temperature TR (s)
A similar kinetic model in used in order to calculate the degradation of a desired food ingredient resulting from pasteurization so the user can assess, as well, the impact of the pasteurization process on the quality of the food .
The equipment purchase cost is calculated as a combination of the the individual costs of the heat exchangers and the holding tube. The heat transfer area is used as the costing variable for the heat exchangers while the volume is used as the costing variable for the holding tube.
1. Wang, D. I. C., C. L.Cooney, A. L.Demain, P. Dunnil, A. E. Humphrey, and M. D. Lilly (1979). Fermentation and Enzyme Technology, John Wiley & Sons.
2. Z.B. Maroulis, Saravacos G.D. (2003). Food Process Dresign, Marcel Dekker, Inc.
3. M. Lewis and Heppel N. (2000). Continuous Thermal Processing of Foods. Pasteurization and UHT Sterilization, Aspen Publishers, Inc., Gaithersburg, Maryland.
4. Dairy processing handbook, Tetra Pak Processing Systems AB, Lund, Sweden.
The interface of this operation has the following tabs:
● Oper. Cond’s, see Pasteurization: Oper. Conds Tab
● Inactivation/Degradation, see Pasteurization: Inactivation/Degradation Tab
● Labor, etc, see Operations Dialog: Labor etc. Tab
● Description, see Operations Dialog: Description Tab
● Batch Sheet, see Operations Dialog: Batch Sheet Tab
● Scheduling, see Operations Dialog: Scheduling Tab