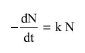
eq. (A.334)
The purpose of this model is to simulate death kinetics in the holding tube of a continuous sterilizer.
● Heat Sterilization Procedure
The death of microorganisms and spores in the holding tube of a continuous heat sterilizer is represented by the following equation (Wang et al, 1979):
|
|
eq. (A.334) |
where N is the concentration of viable organisms (number/L), k is the specific death rate constant (s-1), and t is time (s). At t = t0, N = N0. The specific death rate constant is related to the sterilization temperature by an Arrhenius type of equation:
|
|
eq. (A.335) |
where:
● A is the frequency factor (s-1)
● ΔE is the activation energy of death (cal/mol)
● R is the gas constant (cal/mol-K)
● T is the absolute temperature (K).
The program provides good default values for A, ΔE, R, and T, which the user has the option to modify.
Since actual plug flow through the holding tube of a continuous sterilizer is never achieved, an axial dispersion model is assumed to account for residence time distribution. Solving the material balance equation, we get:
|
|
where:
|
|
eq. (A.337) |
In the above equations, U is the average medium velocity (m/s), L is the length of the holding tube (m), and Dz is the axial dispersion coefficient (m2/s). The latter is estimated as a function of the Reynolds number from the following equation:
|
|
eq. (A.338) |
where:
● μ is the liquid viscosity (kg/m-s)
● ρ is the liquid density (kg/m3)
This equation was derived by fitting experimental data presented in the book of Levenspiel, 1972. The user also has the option to select a simplified plug-flow model.
In design mode of calculation, the sterilization level (N/N0) is specified and the above system of equations is solved with an iterative procedure (i.e., the Secant method) in order to estimate the required tube length (L). In rating mode of calculation, the tube diameter (dt) and length (L) are specified and the system of equations are solved for the the sterilization level (N/N0).
The size estimation of the heat exchangers that are used for energy conservation as well as the estimation of heating and cooling duties under the assumption of a concurrent heat exchange.
The equipment purchase cost includes the cost of the holding tube along with its insulation, the heat exchangers for energy conservation, and the cost of the pumps. Throughput is used as the sizing variable.
1. Wang, D. I. C., C. L.Cooney, A. L.Demain, P. Dunnil, A. E. Humphrey, and M. D. Lilly (1979). Fermentation and Enzyme Technology, John Wiley & Sons.
2. Levenspiel, O. (1972). Chemical Reaction Engineering, 2nd edition, John Wiley & Sons.
The interface of this operation has the following tabs:
● Oper. Cond’s, see Heat Sterilization: Oper. Conds Tab
● Labor, etc, see Operations Dialog: Labor etc. Tab
● Description, see Operations Dialog: Description Tab
● Batch Sheet, see Operations Dialog: Batch Sheet Tab
● Scheduling, see Operations Dialog: Scheduling Tab