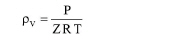
eq. (D.1)
Pure component constants are tabulated by SuperPro Designer in databases, referred to as Physical Properties Databases. In particular, the following three sources of pure component constants are supported:
● the internal database (‘Designer’)
● the Design Institute for Physical Property Research (DIPPR) database
● a user specified database (‘User’)
At present, the following pure component constants:
● Molecular Weight
● Critical Properties (i.e., Critical Pressure, Critical Temperature, Critical Compressibility Factor and Pitzer’s Acentric Factor)
● Standard Gibbs Energy of Formation as an ideal gas at 298.15 K and 1 atm.
● Normal Boiling Point
● Normal Freezing Point
● Liquid density coefficients
● Antoine vapor pressure coefficients
● Ideal gas heat capacity coefficients
● Liquid/solid heat capacity at constant pressure
It is worth noting that the values of pure component constants may sometimes vary between sources as they might have been estimated by different methodologies (with significantly different accuracies) .
Pure component constants (e.g., critical parameters, activity coefficients, Antoine coefficients, enthalpies of vaporization etc.) consist the backbone of VLE modeling.They are essential parameters for the estimation of pure component as well as mixture properties (e.g., K-values, densities, enthalpies) by thermodynamic models (e.g, Raoult’s Law, EOS, etc.). For details, please see the following sections Thermodynamic Properties of Pure Components and Thermodynamic Properties of Mixtures
● Vapor Density
The density (molar volume) of a pure vapor component is calculated by the formula
|
|
eq. (D.1) |
where P is the pressure, R is the gas constant, T is the temperature and Z is the compressibility factor. In the present version of SuperPro, Z=1, or any other words, the vapor is a assumed to behave as an ideal gas.
● Liquid Density
The density of a pure liquid component is calculated as a linear function of temperature
|
|
eq. (D.2) |
● Vapor Heat Capacity
The heat capacity of vapor components is calculated as an ideal gas heat capacity by the following third degree polynomial
|
|
eq. (D.3) |
where the values of the coefficients a, b, c and d are the pure component constants stored in the physical properties database.
● Liquid Heat Capacity
The liquid heat capacity of a pure component is considered tobe independent of the temperature, therefore:
|
|
eq. (D.4) |
where a is a constant stored in the physical properties database.
● Vapor Enthalpy
The enthalpy of a pure component in the vapor phase is calculated (under the assumption of the ideal gas behavior) by the following integral:
|
|
eq. (D.5) |
where TREF is the reference temperature for enthalpy calculations (i.e., the temperature where the enthalpy value is assumed to be zero). The reference temperature is considered a variable of the process file and can be edited by right clicking anywhere in a process file and selecting Ambient, Standard and Enthalpy Ref. Conditions.
● Liquid Enthalpy
The enthalpy of a pure component in the liquid phase is calculated by:
|
|
Notice that the effect of pressure on the enthalpy (i.e., the residual enthalpy) of vapor and liquid components is not currently taken into account in the calculations. This feature will be implemented in a future release of SuperPro.
SuperPro calculates the enthalpy of vaporization of a component at a given temperature, T, by the following empirical correlation:
|
|
eq. (D.7) |
where a is:
|
|
eq. (D.8) |
|
|
eq. (D.9) |
and b is calculated by the generalized Watson correlation (Viswanath and Kuloor, 1967):
Finally ,the enthalpy of vaporization at the normal boiling point of the component is calculated by Chen’s correlation (Chen, 1965)
|
|
eq. (D.10) |
where Tb is the boiling point of the component, Tbr=Tb/Tc is the reduced boiling point and Tc, Pc are the critical temperature and pressure, respectively.
The saturation vapor pressure of a component at temperature T, is calculated by the Antoine equation:
|
|
eq. (D.11) |
where A, B and C are the Antoine coefficients stored in the SuperPro database.
By definition, the fugacity, f, of a pure component is equal to the product of pressure times the species fugacity coefficient, φ:
|
|
eq. (D.12) |
where φ is calculated by the following integral:
|
|
eq. (D.13) |
The term Z in the above equation denotes the compressibility factor which is calculated by the solution of an appropriate cubic EOS. Notice that for most EOS the integral part can be analytically evaluated and so there is no need to apply a numerical integration rule.
● Vapor Density
The density (molar volume) of a vapor mixture is calculated by the formula:
|
|
eq. (D.14) |
where Z is the compressibility factor. In the present version of SuperPro, Z=1 (ideal gas assumption).
● Liquid Density
The liquid density of mixtures is calculated by the ideal mixture model as:
|
|
eq. (D.15) |
where nc is the number of components in the mixture, λi are weight factors (volumetric contribution coefficients) and ρL,i are the pure component liquid densities.
● Vapor Heat Capacity
The heat capacity of a vapor mixture is calculated, under the ideal mixture assumption, as the molar fraction weighted average of pure component ideal gas heat capacities:
|
|
eq. (D.16) |
where yi are their molar fractions of the mixture components and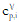 
are the pure-component heat capacities.
● Liquid Heat Capacity
The heat capacity of a liquid mixture is calculated as the molar fraction weighted average of pure component liquid heat capacities:
|
|
eq. (D.17) |
● Vapor Enthalpy
The enthalpy of a vapor mixture is calculated as the molar fraction weighted average of pure component vapor enthalpies.
|
|
eq. (D.18) |
where nc is the number of components in the mixture, yi are the molar fractions of the mixture components and hV,i(T) are the pure species vapor enthalpies. Currently, the effect of the pressure on the enthalpy is neglected. The contribution of residual enthalpy will be implemented in a future release of SuperPro.
● Liquid Enthalpy
The enthalpy of a liquid mixture is calculated as the molar fraction weighted average of pure component liquid enthalpies.
|
|
eq. (D.19) |
where nc is the number of components in the mixture, xi are the molar fractions of the mixture components and hL,i(T) are the pure species liquid enthalpies.
● Vapor Partial Fugacity
The vapor partial fugacity of species i in a mixture, 
, is defined as:
|
|
eq. (D.20) |
where yi is the molar fraction of species i in the mixture and 
is the partial fugacity coefficient, calculated by the integral:
|
|
● Liquid Partial Fugacity
The liquid partial fugacity of species i in a mixture,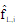 
, of a vapor mixture is defined as:
|
|
eq. (D.22) |
where xi is the molar fraction of species i in the mixture and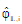 
is the partial fugacity coefficient, calculated by the integral:
|
|
The term Z in and is the compressibility factor, calculated by the solution of an appropriate cubic EOS: the maximum of the three roots obtained is used in while the minimum root is used for . Notice that for most EOS the integral part can be analytically evaluated and so there is no need to apply a numerical integration rule.
A phase-equilibrium ratio is the ratio of molar fractions of a species in the two phases at equilibrium at a given temperature and pressure. For vapor/liquid systems, the constant is referred to as the K-value or vapor/liquid equilibrium ratio:
|
|
eq. (D.24) |
where xi and yi are the molar fractions of component i in the liquid and vapor phase, respectively.
SuperPro supports the following thermodynamic models for the calculation of the K-value.
● Raoult’s Law
The Raoult’s Law assumes ideal behavior for the vapor and liquid phase of the mixture. Under this assumption, the K-value of component i is given by:
|
|
eq. (D.25) |
where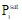 
is the saturation vapor pressure of the pure component i (see Saturation Vapor Pressure), calculated by the Antoine correlation. Notice that with Raoult’s Law, the K-values are independent of the composition of the vapor and liquid phase (i.e., the molar fractions xi and yi). In the case that Antoine coefficients are not available for certain components, SuperPro Designer offers the possibility to bypass the calculation of their K-values by directly setting an expected vapor fraction for them (i.e., the fraction of the component that is expected to be in the vapor phase). This form of hybrid model is only available with Raoult’s Law.
● Modified Raoult’s Law
The Modified Raoult’s Law assumes an ideal vapor phase and a non-ideal liquid phase. The K-value of component i is given by:
|
|
eq. (D.26) |
where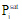 
is the saturation vapor pressure and γL,i is the liquid activity coefficient of component i. Activity coefficients are calculated by an appropriate activity coefficient model (see Activity Coefficient Models).
● Equation of State (EOS)
The EOS expression of the K-value is:
|
|
eq. (D.27) |
where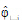 
and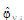 
are the partial fugacity coefficients of species i in the liquid and in the vapor phase, respectively. As explained previously, the partial fugacity coefficients are calculated according to a selected EOS model (see Equations Of State (EOS)).
The employment EOS of state models is a thermodynamically consistent way of calculating the fugacity coefficients of components in the vapor and liquid phase. For example, EOS models have been traditionally used for non-polar mixtures (i.e. hydrocarbons and light gases) at all pressure ranges and for polar mixtures at low pressures only. However, simple EOS models are accurate only in cases of mixtures without strong, special interactions between the molecules of their constituent components. EOS models are known to produce inaccurate results for the liquid phase of mixtures with polar compounds (e.g., acetone+ methanol). This problem is dealt with by the employment of gamma-phi (activity coefficient) models.
● Gamma-Phi Model
The gamma-phi expression of the K-value combines an EOS for the estimation of the vapor phase partial fugacity coefficient and an activity coefficient model for the estimation of the liquid phase partial fugacity coefficient in the liquid phase:
|
|
eq. (D.28) |
where γi is the activity coefficient of component i and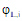 
is the liquid fugacity coefficient of the pure component. The activity coefficients are calculated by an appropriate activity coefficient model (see Activity Coefficient Models).
